📌 Quick Answer
The perpendicular axis theorem states that for a plane (flat) lamina, the moment of inertia about an axis perpendicular to the plane (Iz) equals the sum of the moments of inertia about two mutually perpendicular axes lying in the plane and meeting at the same point: Iz = Ix + Iy.
It applies only to plane laminas and is widely used to find the polar moment of inertia of flat sections.
🔹 Key Takeaways
- Statement: Iz = Ix + Iy, for a plane lamina.
- The z-axis is perpendicular to the lamina; the x and y axes lie in its plane and intersect on the z-axis.
- It applies only to two-dimensional (plane) bodies, not to solid 3D bodies.
- Used to find the polar moment of inertia of shafts and flat sections.
📌 Quick Answer
The perpendicular axis theorem states that for a plane lamina, the moment of inertia about an axis perpendicular to its plane (Iz) equals the sum of the moments of inertia about two mutually perpendicular axes (Ix, Iy) lying in the plane and meeting where the perpendicular axis passes: Iz = Ix + Iy.
It applies only to flat, two-dimensional (planar) bodies such as discs, rings and rectangular plates.
Introduction
The perpendicular axis theorem is a fundamental concept in physics and engineering, which helps us to calculate the moment of inertia of a rigid body about an axis that is perpendicular to the plane of the body. It is one of the most important theorems in rotational mechanics and is widely used in various engineering and scientific applications.
The Perpendicular Axis Theorem states that “The moment of inertia of a planar object about an axis perpendicular to its plane is equal to the sum of the moments of inertia about two perpendicular axes in the plane passing through the same point on the perpendicular axis”.
Definition:
The perpendicular axis theorem states that the moment of inertia of a planar body about an axis perpendicular to the plane of the body is equal to the sum of the moments of inertia of the body about two mutually perpendicular axes lying in the plane of the body and intersecting at the point where the perpendicular axis passes through the plane of the body. Mathematically, it can be written as:
Iz = Ix + Iy
where Iz is the moment of inertia of the body about the perpendicular axis, and Ix and Iy are the moments of inertia of the body about two mutually perpendicular axes lying in the plane of the body.
Derivation:
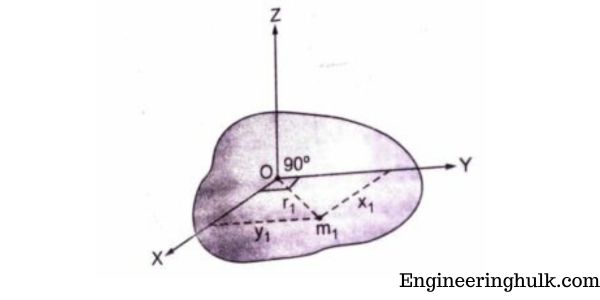
The perpendicular axis theorem can be derived using basic calculus and geometry. Let us consider a planar body of mass M and shape S, which is rotating about a perpendicular axis passing through the origin O. Let us also consider two mutually perpendicular axes X and Y lying in the plane of the body and intersecting at the point P, where the perpendicular axis passes through the plane of the body. Let us assume that the body is rotating with an angular velocity ω.
Now, let us consider an element of mass dm of the body located at a distance r from the origin O. The moment of inertia of this element of mass about the perpendicular axis passing through the origin O is given by:
dIz = r² dm
Similarly, the moment of inertia of this element of mass about the X and Y axes is given by:
dIx = (y² + z²) dm
dIy = (x² + z²) dm
where x, y, and z are the distances of the element of mass from the X, Y, and perpendicular axes, respectively.
Now, let us integrate these equations over the entire body to obtain the moments of inertia of the body about the perpendicular axis and the X and Y axes, respectively:
Iz = ∫S r² dm
Ix = ∫S (y² + z²) dm
Iy = ∫S (x² + z²) dm
By using the Pythagorean theorem, we can simplify these equations as follows:
Ix = Iy = ∫S (x² + y²) dm
Substituting this result into the perpendicular axis theorem equation, we obtain:
Iz = Ix + Iy = 2 ∫S (x² + y²) dm
Using the perpendicular axis theorem, we have reduced the calculation of the moment of inertia about a perpendicular axis to the calculation of the moment of inertia about two mutually perpendicular axes lying in the plane of the body.
Applications:
The perpendicular axis theorem has numerous applications in physics and engineering. Some of its important applications are:
1. Calculating the moment of inertia of a planar body: The perpendicular axis theorem is commonly used to calculate the moment of inertia of a planar body about a perpendicular axis passing through the origin O. By using the theorem, we can reduce the calculation of the moment of inertia to the calculation of the moment of inertia about two mutually perpendicular axes lying in the plane of the body.
2. Understanding the rotation of rigid bodies: The perpendicular axis theorem is fundamental to our understanding of the rotation of rigid bodies. It helps us to determine the moment of inertia of a rigid body with different axes, which is necessary.
Perpendicular Axis Theorem Example
Let’s consider a square plate with a mass of 4 kg and sides of length 2 meters. We want to find the moment of inertia of the square plate about the z-axis passing through its center. To apply the Perpendicular Axis Theorem, we need to find the moments of inertia of the square plate about two perpendicular axes (x and y) in the plane passing through the center of the square.
The moment of inertia of a square plate about its center of mass and perpendicular to its plane (z-axis) is given by:
Iz = (1/6) x m x a²
where m is the mass of the square plate and a is the length of the side of the square plate.
Iz = (1/6) x 4 x (2)²
Iz = 8/3 kg.m²
To find the moments of inertia about the x and y axes, we need to use the parallel axis theorem. According to the parallel axis theorem, the moment of inertia of a planar object about an axis parallel to its plane is equal to the moment of inertia about its center of mass plus the product of its mass and the square of the distance between the two axes.
Ix = Iz + md²
where d is the distance between the center of the square and the x-axis.
From the geometry of the square, we can determine that d = a/2 = 1 meter.
Ix = Iz + md²
Ix = 8/3 + 4 x (1)²
Ix = 20/3 kg.m²
Similarly, the moment of inertia about the y-axis passing through the center of the square can be found using the same formula:
Iy = Iz + md²
where d is the distance between the center of the square and the y-axis, which is also equal to a/2.
Iy = Iz + md²
Iy = 8/3 + 4 x (1)²
Iy = 20/3 kg.m²
Finally, we can apply the Perpendicular Axis Theorem to find the moment of inertia of the square plate about the z-axis.
Iz = Ix + Iy
Iz = 20/3 +20/3
Iz =40/3
Also, read the strain formula
Frequently Asked Questions
State the perpendicular axis theorem.
For a plane lamina, the moment of inertia about an axis perpendicular to the plane equals the sum of the moments of inertia about two perpendicular axes in the plane: Iz = Ix + Iy.
Does the perpendicular axis theorem apply to 3D bodies?
No. It is valid only for plane (two-dimensional) laminae, not for three-dimensional solid bodies.
Give an example of the perpendicular axis theorem.
For a circular disc, the moment of inertia about the central perpendicular axis is Iz = ½MR². By symmetry Ix = Iy, so Ix = Iy = ¼MR².
How is it different from the parallel axis theorem?
The parallel axis theorem (I = Icm + Md²) shifts an axis parallel to one through the centre of mass; the perpendicular axis theorem relates three mutually perpendicular axes of a plane lamina.
Frequently Asked Questions
What is the perpendicular axis theorem?
For a plane lamina, the moment of inertia about an axis perpendicular to the plane equals the sum of the moments of inertia about two perpendicular axes in the plane that meet at the same point (Iz = Ix + Iy).
What is the difference between the parallel and perpendicular axis theorems?
The perpendicular axis theorem (Iz = Ix + Iy) applies to plane laminas, while the parallel axis theorem (I = Ig + Ad squared) shifts the axis of any body to a parallel axis a distance away from the centroid.
Does the perpendicular axis theorem apply to 3D bodies?
No. It is valid only for plane (two-dimensional) laminas, because it assumes all mass lies in one plane.
Where is the perpendicular axis theorem used?
To find the polar moment of inertia of shafts and flat sections, which is needed in torsion and in the design of rotating components.
Related Topics on EngineeringHulk
- 👉 Moment of Force – Calculation & Types
- 👉 Torsion of Shafts – Study Guide
- 👉 Strength of Materials – Study Guide
1 thought on “Perpendicular Axis Theorem – Definition & Application”