The Pythagorean theorem: A detailed view of the Pythagorean

Table of Contents

Definition:

The Pythagorean theorem is a mathematical theorem that states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.

The theorem is named after the ancient Greek mathematician Pythagoras. The theorem can be written as an equation: a2 + b2 = c2, where a and b are the lengths of the two sides of the triangle, and c is the length of the hypotenuse.

This equation is known as the Pythagorean equation. It is also sometimes referred to as the “Pythagorean identity”. The Pythagorean theorem is one of the most well-known theorems in mathematics and is used in many mathematical fields, including geometry, trigonometry, and algebra.

It is also used in everyday life, for example, to calculate the length of the hypotenuse of a triangle when the lengths of the other two sides are known. It is also used in architecture and engineering to calculate the length of beams, columns, walls, and other structures.

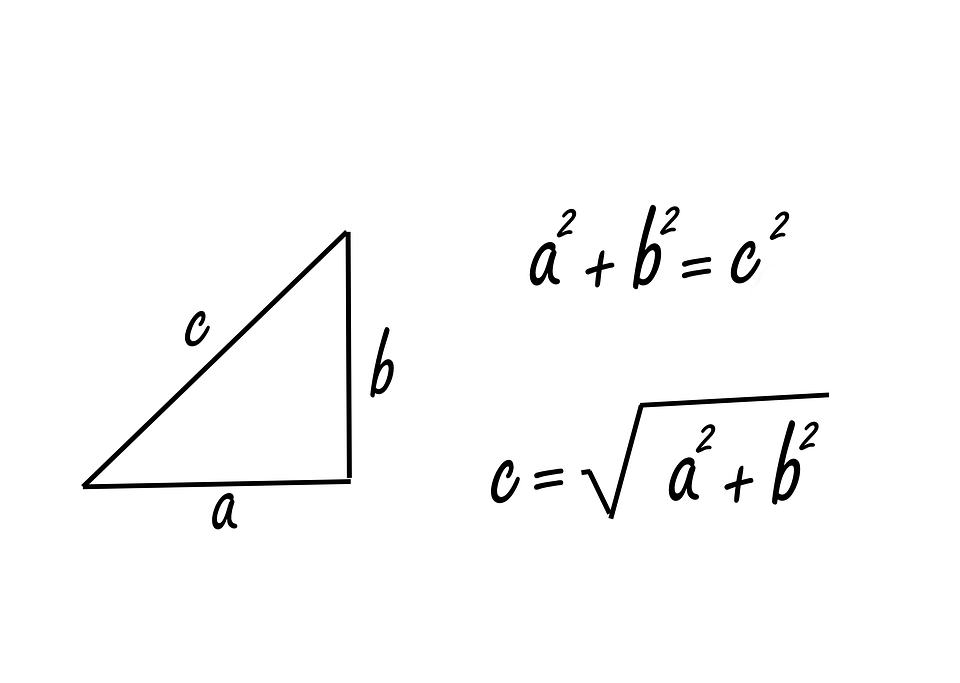
Solved Examples:

Here are two solved problems involving the Pythagorean theorem:

Question 1: A right-angled triangle has one leg measuring 6 cm and the other measuring 8 cm. Find the length of the hypotenuse.

Answer 1:

To solve for the hypotenuse (let’s call it ( c )), we can use the Pythagorean theorem:
[ a^2 + b^2 = c^2 ]

Given: ( a = 6 ) cm and ( b = 8 ) cm
[ c^2 = 6^2 + 8^2 ]
[ c^2 = 36 + 64 ]
[ c^2 = 100 ]

To find ( c ), take the square root of both sides:
[ c = \sqrt{100} ]
[ c = 10 ] cm

So, the length of the hypotenuse is 10 cm.

Question 2: In a right triangle, the hypotenuse measures 15 cm, and one of the legs is 9 cm. Find the length of the other leg.

Answer 2:

Let’s call the unknown leg ( b ). Using the Pythagorean theorem:
[ a^2 + b^2 = c^2 ]

Given: ( a = 9 ) cm and ( c = 15 ) cm
[ b^2 = 15^2 – 9^2 ]
[ b^2 = 225 – 81 ]
[ b^2 = 144 ]

To find ( b ), take the square root of both sides:
[ b = \sqrt{144} ]
[ b = 12 ] cm

So, the length of the other leg is 12 cm.

The uses of the Pythagorean theorem:

The Pythagorean theorem is a fundamental principle in geometry that states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. Specifically:

[ c^2 = a^2 + b^2 ]

where ( c ) is the length of the hypotenuse and ( a ) and ( b ) are the lengths of the other two sides.

The theorem has a myriad of applications, both within mathematics and in practical situations. Here are some of the uses of the Pythagorean theorem:

Basic Geometry: It’s used to determine the length of one side of a right triangle when the lengths of the other two sides are known.
Distance Between Two Points: In the Cartesian coordinate system, the Pythagorean theorem can be used to find the distance between two points.
Trigonometry: The theorem is foundational in trigonometry, particularly when defining the fundamental trigonometric relationships.
Construction and Design: Architects and engineers use the theorem when designing and constructing buildings, bridges, and other structures to ensure right angles and to calculate distances indirectly.
Computer Graphics: The theorem helps in calculating distances and angles between pixels, and is used in algorithms for rendering shadows, reflections, and more.
Navigation and GPS: The theorem can help in determining the shortest path between two points, and it’s used in more complex three-dimensional scenarios in aviation and space navigation.
Physics: In problems involving vectors, especially those in two or three dimensions, the theorem can be used to determine resultant magnitudes.
Astronomy: Astronomers use the theorem to calculate distances between stars and other celestial bodies when using parallax methods.
Surveying: Surveyors use the theorem to determine distances indirectly, especially when measuring land.
Gaming: Developers utilize the theorem in programming game physics, especially where distance and angle calculations are critical.
Error Detection: In digital communications, a two-dimensional representation of signals (I-Q diagram) might use the Pythagorean theorem to detect errors.
Machine Learning and Data Mining: In clustering algorithms like K-means, the theorem can be used to calculate the distance between data points in a multi-dimensional space.
Sports: For example, in baseball, to determine how far a player has to throw from one base to another in a diagonal.
Circuit Analysis: In electrical engineering, when dealing with AC circuits, the theorem can be used in combination with complex numbers to analyze circuit behavior.

This list is by no means exhaustive. The Pythagorean theorem is one of the cornerstones of geometry, and its applications permeate multiple domains, from pure mathematics to a wide array of practical fields.

How to solve the Pythagorean theorem:

The Pythagorean theorem is a mathematical equation used to find the length of the sides of a right triangle. The equation is written as a2 + b2 = c2, where a and b are the lengths of the two legs of the triangle and c is the length of the hypotenuse.

To solve the Pythagorean theorem, the first step is to identify which side you are trying to find the length of. Then, you will need to use the equation to solve for the unknown side.

For example, if you are trying to find the length of the hypotenuse, you will use the equation c2 = a2 + b2. To solve for c, you will need to know the lengths of the other two sides, a and b.

Once you have those values, you can plug them into the equation and solve for c. If you are trying to find the length of one of the other two sides, you will use the equation a2 + b2 = c2.

To solve for either a or b, you will need to know the length of the other side, as well as the length of the hypotenuse. Once you have those values, you can plug them into the equation and solve for either a or b.

Once you have solved the unknown side, you will have the length of the side you were looking for. This is how you solve the Pythagorean theorem.