Table of Contents
Introduction:
The parallelogram law of forces is a fundamental principle in physics that describes how two forces acting at a point can be combined to create a resultant force. This law is essential for understanding the mechanics of structures and machines, as well as for analyzing the forces acting on objects in motion.
What is the Parallelogram Law of Forces?
The parallelogram law of forces states that “if two forces acting on a point are represented by two adjacent sides of a parallelogram, then their resultant force is represented by the diagonal passing through the point”. This means that the resultant force is equal in magnitude and direction to the diagonal of the parallelogram formed by the two forces.
In other words, the parallelogram law of forces formula allows us to calculate the magnitude and direction of the resultant force when two forces acting at an angle to each other are combined.
Derivation of the Parallelogram Law of Forces Formula
The parallelogram law of forces formula can be derived using the principles of vector addition. Consider two forces F1 and F2 acting at a point O as shown in the figure below.
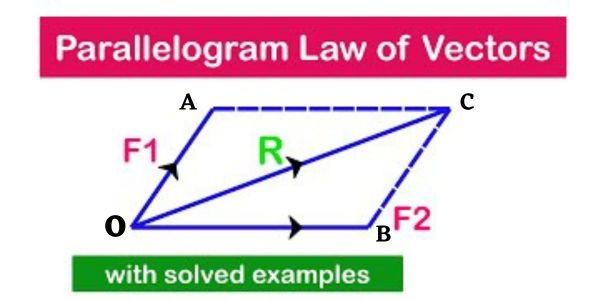
To calculate the resultant force, we draw the vectors F1 and F2 as adjacent sides of a parallelogram OABC. The diagonal OC passing through point O represents the resultant force both in magnitude and direction.
The vector OC can be calculated using the following formula:
OC = √(OA² + AC² + 2OA.AC cosθ)
where OA and AC are the magnitudes of F1 and F2, respectively, θ is the angle between the two forces, and cosθ is the cosine of the angle between the two forces.
The direction of the resultant force can be determined using the following formula:
tanα = (AC sinθ)/(OA + AC cosθ)
where α is the angle between the resultant force and the force F1.
**Examples of Application of the Parallelogram Law of Forces Formula**
Let’s consider some examples to see how the parallelogram law of forces formula is applied in practice.
Example 1: Two forces F1 and F2 of magnitudes 10 N and 8 N, respectively, act on a point O at an angle of 60 degrees to each other. Calculate the magnitude and direction of the resultant force.
Using the parallelogram law of forces formula, we can calculate the magnitude of the resultant force as follows:
OC = √(OA² + AC² + 2OA.AC cosθ)
= √(10² + 8² + 2x10x8xcos60)
= √(100 + 64 + 80)
= √(244)
= 15.62 N
The direction of the resultant force can be calculated as follows:
tanα = (AC sinθ)/(OA + AC cosθ)
= (8 sin60)/(10 + 8 cos60)
= 0.83
Therefore, α = tan⁻¹(0.83) = 39.33 degrees.
Hence, the magnitude and direction of the resultant force are 15.62 N and 39.33 degrees, respectively.
Applications of the Parallelogram Law of Forces
The parallelogram law of forces has numerous applications in various fields of science and engineering. Some of these applications are discussed below.
1. Structural Engineering
In structural engineering, the parallelogram law of forces is used to calculate the forces acting on a structure, such as a bridge or a building. By analyzing the forces acting on each component of the structure, engineers can determine the stresses and strains that the structure can withstand.
2. Mechanical Engineering
In mechanical engineering, the parallelogram law of forces is used to calculate the forces acting on machines and mechanical systems. By understanding the forces acting on each component of a machine, engineers can design machines that are efficient and safe to use.
3. Physics
In physics, the parallelogram law of forces is used to analyze the motion of objects under the influence of multiple forces. By understanding the resultant force acting on an object, physicists can predict its motion and calculate its velocity and acceleration.
4. Aviation
In aviation, the parallelogram law of forces is used to calculate the forces acting on an aircraft. By analyzing the forces acting on the wings and other components of an aircraft, engineers can design planes that are aerodynamically stable and safe to fly.
Also, read the hardness test