Table of Contents
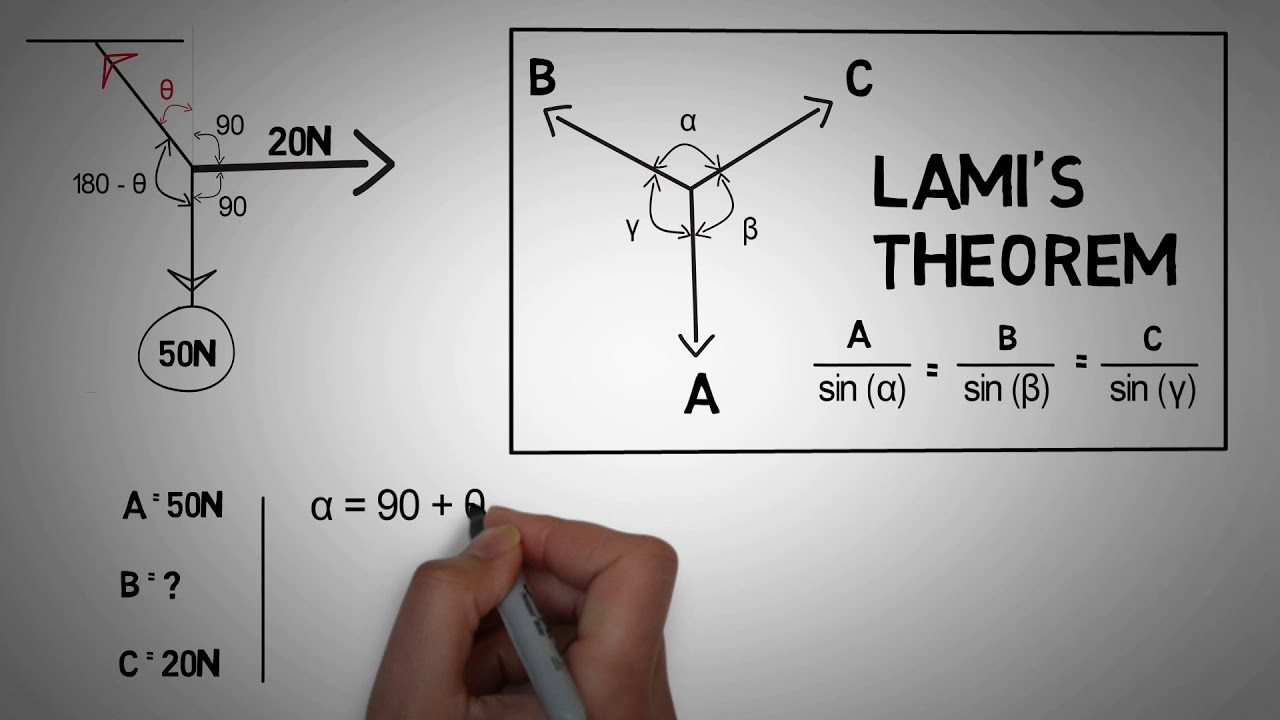
The definition of Lami’s Theorem:
Lami’s Theorem is a mathematical theorem stating that the angles in any triangle sum 180 degrees. This theorem is also known as the “triangle angle sum theorem,” and it is one of the most important theorems in geometry.
It is named after the Italian mathematician Giovanni Girolamo Saccheri (1667–1733), who is credited with first proving this theorem. The theorem states that the sum of a triangle’s interior angles equals 180 degrees.
This means that the three angles that make up a triangle, when added together, equal 180 degrees. This theorem is true for both right and oblique triangles and all other types of triangles.
This theorem is an important part of Euclidean geometry and is used in many areas of mathematics, including trigonometry, calculus, and even algebra. It is also used to calculate the area of a triangle and the lengths of the sides of a triangle.
This theorem is important in many other fields, such as architecture, engineering, and even physics. In addition, Lami’s theorem is also used to solve many problems in geometry and other related fields.
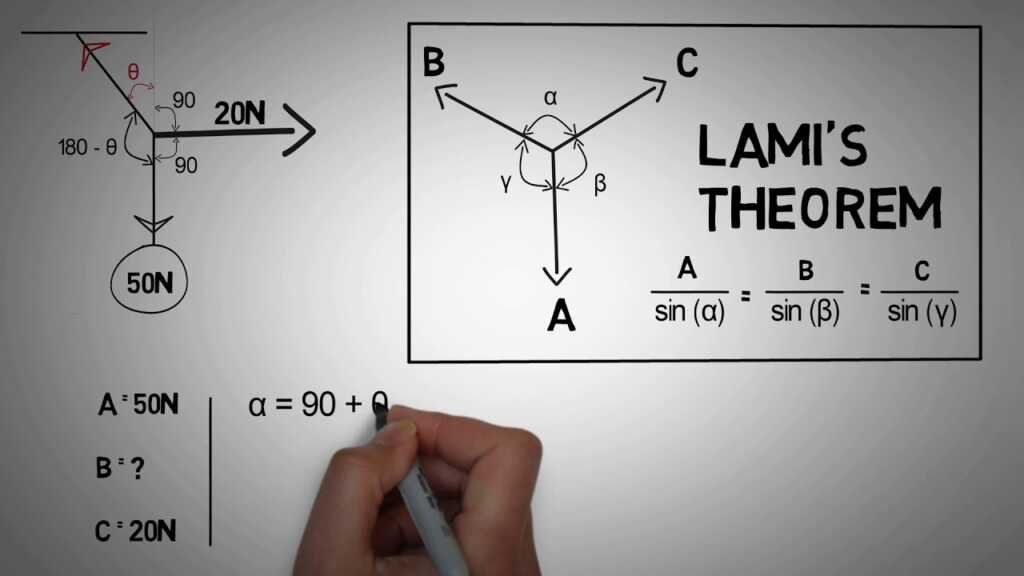
Proof of Lami’s Theorem:
Lami’s Theorem is a mathematical theorem that states that the sum of a triangle’s angles equals two right angles. It was named after the Italian mathematician Giovanni Lami, who first proposed it in 1750.
The theorem states that in any triangle, the sum of the three angles is equal to two right angles, or 180°. This means that the three angles of a triangle must add up to 180°.
This is true for any triangle, no matter what the size of the angles or the lengths of the sides. To prove this theorem, we can use the properties of triangles. First, we must draw a triangle and label the angles as A, B, and C.
Then, we can use the Triangle Angle Sum Theorem, which states that the sum of the interior angles of a triangle is equal to 180°. Next, we can use the Triangle Angle Bisector Theorem, which states that if the three angles of a triangle are bisected, the resulting angles are all equal.
This means that if we bisect each of the angles A, B, and C, we will get three equal angles, each half of which is the original angle. Finally, we can use the Triangle Inequality Theorem, which states that the sum of any two sides of a triangle must be greater than the third side.
This means that if we add up the three bisected angles, they must be greater than the third angle. Combining these three theorems, we can conclude that the sum of the three angles of a triangle is equal to two right angles, or 180°. Therefore, Lami’s Theorem is true.
The Mathematical Formulation of Lami’s theorem:
Lami’s theorem is an important theorem in plane geometry that states: “The three angle bisectors of the angles of a triangle intersect in a single point.”
This theorem can be expressed mathematically as A+B+C = 180° Where A, B, and C are the angles of the triangle. In addition, the angle bisectors of A, B, and C meet at a single point (x,y) in the plane.
This can be expressed mathematically as A1+A2=A B1+B2=B C1+C2=C Where A1, A2, B1, B2, C1, and C2 are the angles of the angle bisectors.
Finally, the point of intersection (x,y) can be calculated as follows: x = (A1x1 + A2x2 + B1y1 + B2y2 + C1z1 + C2z2)/(A1+A2+B1+B2+C1+C2) y = (A1y1 + A2y2 + B1x1 + B2x2 + C1z1 + C2z2)/(A1+A2+B1+B2+C1+C2) Where x1, y1, x2, y2, z1, and z2 are the coordinates of the points of the triangle.
This is the mathematical formulation of Lami’s theorem.
The applications of Lami’s Theorem:
Lami’s Theorem is a theorem in the field of geometry, named after the Italian mathematician Giovanni Lami. It states that if a triangle ABC is trisected by the lines AD, BE, and CF, then the following equation holds true:
AB^2 + AC^2 + BC^2 = AD^2 + BE^2 + CF^2. This theorem has a variety of applications in mathematics, science, engineering, and other fields. One of the most common applications is in problem-solving, where it can be used to solve a variety of triangle problems.
For example, it can be used to find the area of a triangle when the lengths of three of its sides are known. It can also be used to find the length of the sides of a triangle when the area and two sides are known, or the length of one side when the area and the other two sides are known.
In addition, Lami’s Theorem is also useful for deriving equations for complex shapes, such as circles or ellipses. It can be used to derive equations for inscribed shapes, such as a circle inscribed in a triangle. It can also be used for deriving equations for circumscribed
Also, read Byopia/biopia