Table of Contents
Kinematics is a branch of physics that studies the motion of objects without considering the forces that cause the motion. It provides us with a set of mathematical equations known as kinematic equations, which help us understand and describe the motion of objects accurately.
What are Kinematic Equations?
Kinematic equations are mathematical expressions that relate the variables of motion, such as displacement, velocity, acceleration, and time. They provide a framework for quantifying the characteristics of an object’s motion and predicting its future behavior. The fundamental kinematic equations are derived from basic principles, allowing us to solve a wide range of motion-related problems.
Types of Kinematic Equations:
There are three primary types of kinematic equations, each focusing on a specific aspect of an object’s motion:
a) Equations for Uniformly Accelerated Motion:
These equations are applicable when an object experiences constant acceleration. They are commonly used in scenarios involving free-falling bodies or objects subjected to constant forces. The equations for uniformly accelerated motion are as follows:
– Displacement (s) = ut + (1/2)at^2
– Final Velocity (v) = u + at
– Final Velocity squared (v^2) = u^2 + 2as
– Displacement (s) = ((u + v)/2) * t
Where:
– s: Displacement
– u: Initial velocity
– v: Final velocity
– a: Acceleration
– t: Time
b) Equations for Uniform Motion:
These equations apply when an object moves with a constant velocity (zero acceleration). Uniform motion equations are useful in situations where the object’s acceleration is negligible or canceled out by opposing forces. The equations for uniform motion are as follows:
– Displacement (s) = ut
– Final Velocity (v) = u
– Time (t) = s/u
Where:
– s: Displacement
– u: Initial velocity
– v: Final velocity
– t: Time
c) Equations for Free Fall:
Free fall equations specifically deal with objects in vertical motion under the influence of gravity. Since the only significant force acting on the object is gravity, acceleration due to gravity (g) is taken as a constant. The equations for free fall are:
– Displacement (s) = ut + (1/2)gt^2
– Final Velocity (v) = u + gt
– Time of Flight (t) = (v – u)/g
Where:
– s: Displacement
– u: Initial velocity
– v: Final velocity
– g: Acceleration due to gravity
– t: Time
Rotational Kinematic Equations: Formulas and Applications
1. What are Rotational Kinematic Equations?
Rotational kinematic equations are mathematical expressions that relate the variables associated with rotational motion, such as angular displacement, angular velocity, angular acceleration, and time. These equations enable us to quantify and analyze the characteristics of objects that rotate or spin around a fixed axis. They play an important role in fields like physics, engineering, and mechanics, where understanding rotational motion is essential.
2. Types of Rotational Kinematic Equations:
a) Equation for Angular Displacement (θ):
The angular displacement of an object represents the change in its rotational position. The equation for angular displacement is:
– θ = ω_i * t + (1/2) * α * t^2
Where:
– θ: Angular displacement
– ω_i: Initial angular velocity
– α: Angular acceleration
– t: Time
b) Equation for Angular Velocity (ω):
Angular velocity describes the rate at which an object rotates. The equation for angular velocity is:
– ω = ω_i + α * t
Where:
– ω: Angular velocity
– ω_i: Initial angular velocity
– α: Angular acceleration
– t: Time
c) Equation for Angular Acceleration (α):
Angular acceleration represents the rate at which the angular velocity of an object changes. The equation for angular acceleration is:
– ω = ω_i + α * t
Where:
– α: Angular acceleration
– ω_i: Initial angular velocity
– ω: Final angular velocity
– t: Time
d) Equation for Centripetal Acceleration (a):
Centripetal acceleration refers to the acceleration experienced by an object moving in a circular path. The equation for centripetal acceleration is:
– a = ω^2 * r
Where:
– a: Centripetal acceleration
– ω: Angular velocity
– r: Radius of the circular path
Applications of Kinematic Equations:
1. Automotive Engineering:
In the field of automotive engineering, kinematic equations play a crucial role in designing and optimizing vehicle dynamics. By applying kinematic equations, engineers can analyze the motion of automobiles, including acceleration, velocity, and braking. This information is valuable for enhancing vehicle safety, performance, and fuel efficiency. Kinematic equations also aid in the development of advanced driver-assistance systems (ADAS), such as adaptive cruise control and collision avoidance systems.
2. Aerospace and Aviation:
In the aerospace and aviation industries, kinematic equations are essential for understanding the flight dynamics of aircraft, rockets, and satellites. These equations enable engineers to calculate the trajectory, velocity, and acceleration of objects in flight.
By incorporating kinematic equations into their designs, aerospace engineers can ensure optimal launch trajectories, fuel efficiency, and precise landing procedures. Kinematic equations are also vital in orbital mechanics, allowing scientists to predict the paths of satellites and spacecraft.
3. Sports Biomechanics:
Kinematic equations have a significant impact on sports biomechanics, helping researchers and coaches analyze the movements of athletes. By utilizing motion capture technology and applying kinematic equations, scientists can precisely measure and quantify variables such as speed, acceleration, and trajectory in sports like running, swimming, and gymnastics.
This data aids in performance analysis, injury prevention, and technique optimization, ultimately leading to improved athletic performance.
4. Robotics and Automation:
In the field of robotics and automation, kinematic equations are indispensable for controlling the motion of robotic arms, manipulators, and automated systems. By integrating kinematic equations into the control algorithms, engineers can accurately determine the position, velocity, and acceleration of robotic components.
This allows for precise movement planning, path optimization, and collision avoidance, enhancing the efficiency and safety of robotic systems used in manufacturing, healthcare, and exploration.
5. Video Game Development:
Kinematic equations also find applications in the development of realistic and immersive video games. Game designers and programmers employ kinematic equations to simulate the motion of characters, objects, and vehicles within virtual environments. By accurately modeling the laws of motion using kinematic equations, game developers can create more authentic and engaging gameplay experiences, enhancing player immersion and realism.
6. Civil Engineering:
In civil engineering, kinematic equations are utilized to analyze the behavior and stability of structures subjected to dynamic forces. Engineers apply these equations to study the movement of bridges, buildings, and other infrastructure elements, ensuring their safety and structural integrity.
By incorporating kinematic equations into their calculations, civil engineers can accurately predict the response of structures to various loads and vibrations, optimizing their designs and preventing potential failures.
7. Rotational kinematic equations find applications in various fields, including:
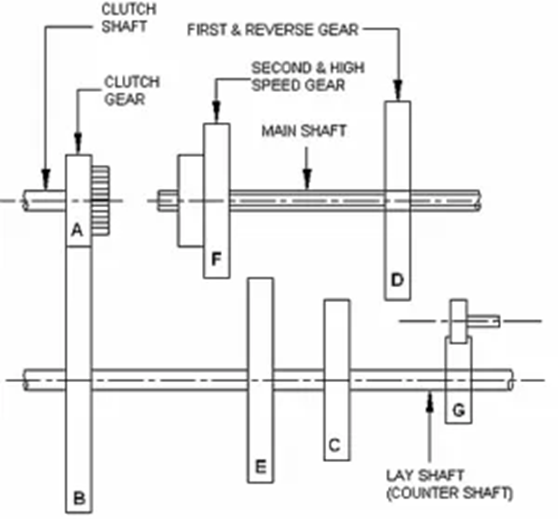
– Mechanics: Used to study the motion of rotating objects, such as gears, wheels, and flywheels.
– Physics: Applied to analyze the behavior of rotating systems, such as the motion of planets and satellites.
– Engineering: Employed in designing and analyzing rotational machineries, such as turbines and motors.
– Robotics: Utilized to model and control the movements of robot arms and manipulators.
Also, read Mansa Musa