Table of Contents
EXAMINATION OF AERODYNAMIC FORCES ACTING ON THE BLADE
Aerodynamic forces acting on a blade component tending to the kind it rotates, are significant limits for a classification engineer. These are several basic kinds of blades on aero turbine may have, e.g., sails, planes and aerodynamic surfaces based on the aircraft wing cross-section for which there are numerous kinds. The early history of windmills is founded on the first two; current higher effectiveness wind-electric generators are founded on the usage of blades with aerodynamic surfaces.
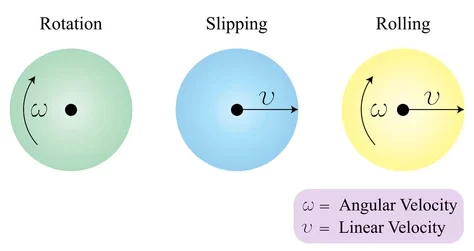
The blade can break through as a characteristic cross-section portion of a two-bladed aero turbine. The element publicized is at around radius ‘r’ from the axis of rotation. It is affecting the left. Since the blade is affecting the plane of rotation it sees a peripheral wind velocity, VT, in the plane of revolution.
This component additional vectorially to the imposing wind velocity stretches the subsequent wind velocity, VR, seen by the revolving blade component. At right viewpoints to VR, is the lift force FL, produced by the aerodynamic figure of the blade. The drag force, FD is equivalent to VR. The vector sum of FL and FD is FR which has a rotation producing component, FT and a thrust producing constituent. The former drives the aero-turbine rotationally and the advanced tends to flex and inversion the aerogenerator. The centred of the centre of lift of the aerodynamic blade is a vector diagram.
As is well known from aircraft wind philosophy, one of the critical boundaries is’’ the viewpoint of attack of the aerodynamic element. It controls lift and drag forces and hence the speed and torque productivity of the aero turbine. These sums can be varied by changing the blade pitch angle ‘β’, and this is the basis rotation control method rummage-sale on large variable pitch wind-electric generators. The torque would control the AC output power if a synchronic generator was used.
Since VT, upsurges linearly as we go out identical, ‘or, on a motivated aero turbine blade, it is compulsory to regulate ‘β’ with ‘r’ to always have a positive angle of attack and to uphold sensible stress/pressure levels within the blade. This means that at large ‘r’, ‘β’ is made minor while at small ‘r’, ’β’ is large. Thus, the blade ‘bites’ the air additional in close than near the tips. These deliberations result in an aero turbine blade with an ostensible twist in it. The need for twisting windmills sails was recognised hundreds of years ago and extensively used on Dutch windmill.
Having now accomplished an elementary understanding of the basics of what turns the aero turbine, we see that the airfoil alignment for an aero turbine energy by the wind is exactly opposite to the positioning of a classical aeroplane propeller which is mechanically driven and whose purpose is to go give a lift force in the axial direction. Thus, kaput aircraft wing theory applies to the operation of an aero turbine, direct of a traditional aircraft propeller on an aero turbine, would not produce the maximum efficient aero turbine because the aerodynamic outward is oriented backwards to what it must be.
CONCERT OF WIND MACHINES
WECS efficiency is of attention to both aerogenerator designers and system engineers. As WECS is a capital-intensive skill, it is wanted for the complete wind electric plant to have the uppermost efficiency possible, thus optimally utilizing capital capitals and minimizing the busbar electric energy value.
The complete conversion efficiency, µoof an aerogenerator of the universal type, is,
Directly above equation shows an application of cascaded energy adaptation, from which overall efficacy will be strongly resolute by the lowermost efficiency evangelist in the cascade. For the aerogenerator this is the aero turbine; the effectiveness of the remaining three elements can be made quite high but less than 100 per cent. It is now apparent why so much importance is placed on the efficacy of the aero turbine in wind literature. Analysis of Aerodynamic forces acting on windmill blades
Consider a subjective aero turbine (Here Aero turbine is not equivalent to an aerogenerator) of cross-sectional area ‘A’ driven by the wind. Its efficiency would be:
Thus, the coefficient of the concert of an aero turbine is the fraction of power in the wind through the brushed area which is converted into useful mechanical shaft power. The coefficient of performance is widely employed throughout the fresh wind research. We have seen that Cp for horizontal axis wind machine has theoretical extreme value = 0.593.
Analysis of Aerodynamic forces acting on windmill blades
This theoretical efficacy constraint on a wind energy adaptation system is loosely analogical comparable to the thermodynamic Carnot efficacy constraint on a conventional thermal power plant.
We know that the exchangeable power of energy is comparative to the cube of wind speed. Thus, if the wind swiftness decreases by 20%, the power output is concentrated by almost 50%. The wind swiftness may very substantial from day to day and from season to season. The efficiency of a wind generator depends on the enterprise of a wind rotor and rotational speed, expressed as the ratio of blade landfill speed to wind speed i.e., VT/V (is called as Tip Speed Ratio – TSR), if n is the revolution frequency, i.e., rotation per second, if a propeller diameter D meters, the tip speed is πND m/sec.
We know that the exchangeable power of energy is comparative to the cube of wind speed. Thus, if the wind swiftness decreases by 20%, the power output is concentrated by almost 50%. The wind swiftness may very substantial from day to day and from season to season. The efficiency of a wind generator depends on the enterprise of a wind rotor and rotational speed, expressed as the ratio of blade landfill speed to wind speed i.e., VT/V (is called as Tip Speed Ratio – TSR), if n is the revolution frequency, i.e., rotation per second, if a propeller diameter D meters, the tip speed is πND m/sec.
AERODYNAMIC FORCES ACTING ON THE BLADE
The requirement of the power co-efficient on the tip speed ratio (TSR) for some mutual rotor types. It is seen that the two-bladed propeller/paddle type of rotor can achieve a much higher power co-efficient (i.e., it is the more efficient) than the American mechanism multi-blade windmill and the classical Dutch four-bladed windmill. In practice two-bladed propeller (horizontal axis) rotor are originate to attain a supreme power co-efficient of 0.40 to 0.45 at a tip speed ratio in the range a roughly 6 to 10 Golding consumes resulting in the appearance for aero turbine efficiency as, Clearly If here was no drag, i.e., K=0, then efficiency would be agreement (μA=1).
In practicality, K can be made very small, liable on the airfoil chosen and the angle of attack. Also, the above calculation tells us the efficiency would be low if VT/V were very huge or again If it were minor. One suspicion that there exists an optimal ratio of VT/V (i.e., TSR).
If one accumulates mock-ups of numerous types of aero turbine blades and puts them in a wind passageway and runs carefully measured experiments of their efficacies as the purpose of their TSR’S, then 1 attains a family of curves similar.
The various types of windmills recital appearances with respect to TSR and torque co-efficient.
Only at transitional wind speed does the system effectiveness reach it’s optimum and the power removed then follows a V3 law. The range of optimum operation depends on the engine selected to give optimal output over the year. Considering or seeing the range of wind speed is 10-14m/sec, 14m/sec being the rated velocity preserved also at advanced wind speeds. Only their contingent on the degree of complexity could be between 70 and 85% of the exchangeable wind energy by the gear type broadcast, which connects the rotor shaft to the electric generator.